Math Portal
Introductory Statistics
Section 2.4 - Basic Probability Concepts
Probability is ongoing in everyday life. It is used in determining casino gaming payoffs, weather predictions, tables of life expectancy, airline baggage loss expectations, and numerous other chance occurrences. This chapter will introduce the basic terminology and concepts that you must know in order to understand and calculate probabilities.
Sample Spaces
A random experiment is a process that gives a single result that cannot be determined beforehand. Examples of simple random experiments are tossing a fair die one time and observing the up face; flipping a fair coin one time and observing the up face; and drawing one card at random from a well-shuffled deck of cards and observing which card was drawn. Each of these experiments yields a single result that occurs randomly. In each case, you can expect one of a number of possible results. Each individual possible result is called an outcome of the experiment. For instance, in the random experiment of tossing a fair die one time and observing the up face, the six possible outcomes are the following: one dot is on the up face, two dots are on the up face, three dots are on the up face, four dots are on the up face, five dots are on the up face, and six dots are on the up face.
A sample space, S, is the set of all possible outcomes of an experiment. Each member of S is called an outcome (or simple event, sample point, or elementary outcome). For instance, if you were performing a random experiment of tossing a fair die where 1 represents the outcome that the die shows one dot on the up face, 2 represents the outcome that the die shows two dots on the up face, and so on, the sample space would be, S = {1, 2, 3, 4, 5, 6}.
If you were rolling two dice, the sample space would be, S = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12|.
Sometimes an experiment consists of several stages. For instance, consider the experiment of flipping three fair coins and observing the up face on each. You can think of this experiment as having three stages: flipping the first coin and observing the up face, flipping the second coin and observing the up face, and flipping the third coin and observing the up face. From the Fundamental Counting Principle, you know there are 2∙2∙2 = 8 outcomes for this experiment. The sample space for this experiment is {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}, where H in the first position means Heads on the first coin, H in the second position means Heads on the second coin, H in the third position means Heads on the third coin, T in the first position means Tails on the first coin, and so on.
For some experiments, listing and counting the outcomes in the sample space is easy, as in the previous examples. In other experiments, especially those consisting of several stages, you will have to rely on counting techniques to determine the number of outcomes in the sample space.
EXAMPLE: Standard decks of 52 playing cards consists of four suits: clubs ♣, spades ♠, hearts ♥, and diamonds ♦. Clubs and spades are black-colored suits; hearts and diamonds are red-colored suits. Each suit has 13 cards consisting of 3 face cards (king, queen, and jack) and number cards from 1 (ace) to 10.

Consider the experiment of drawing 5 cards at random from a well-shuffled deck of 52 playing cards. How many outcomes are in the sample space of this experiment?
SOLUTION: Since the order in which the five cards are arranged after they are drawn is not important in the problem, this is a combination problem. You want to know how many different 5-card combinations are possible when drawing from a deck of 52 playing cards. Therefore, you need to calculate the combination of 5 items selected from 52 distinct items
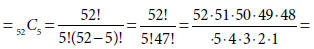
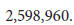
Thus, in the experiment of drawing 5 cards from a standard deck of 52 playing cards, the number of outcomes in the sample space is 2,598,960.
Probability is ongoing in everyday life. It is used in determining casino gaming payoffs, weather predictions, tables of life expectancy, airline baggage loss expectations, and numerous other chance occurrences. This chapter will introduce the basic terminology and concepts that you must know in order to understand and calculate probabilities.
Sample Spaces
A random experiment is a process that gives a single result that cannot be determined beforehand. Examples of simple random experiments are tossing a fair die one time and observing the up face; flipping a fair coin one time and observing the up face; and drawing one card at random from a well-shuffled deck of cards and observing which card was drawn. Each of these experiments yields a single result that occurs randomly. In each case, you can expect one of a number of possible results. Each individual possible result is called an outcome of the experiment. For instance, in the random experiment of tossing a fair die one time and observing the up face, the six possible outcomes are the following: one dot is on the up face, two dots are on the up face, three dots are on the up face, four dots are on the up face, five dots are on the up face, and six dots are on the up face.
A sample space, S, is the set of all possible outcomes of an experiment. Each member of S is called an outcome (or simple event, sample point, or elementary outcome). For instance, if you were performing a random experiment of tossing a fair die where 1 represents the outcome that the die shows one dot on the up face, 2 represents the outcome that the die shows two dots on the up face, and so on, the sample space would be, S = {1, 2, 3, 4, 5, 6}.
If you were rolling two dice, the sample space would be, S = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12|.
Sometimes an experiment consists of several stages. For instance, consider the experiment of flipping three fair coins and observing the up face on each. You can think of this experiment as having three stages: flipping the first coin and observing the up face, flipping the second coin and observing the up face, and flipping the third coin and observing the up face. From the Fundamental Counting Principle, you know there are 2∙2∙2 = 8 outcomes for this experiment. The sample space for this experiment is {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}, where H in the first position means Heads on the first coin, H in the second position means Heads on the second coin, H in the third position means Heads on the third coin, T in the first position means Tails on the first coin, and so on.
For some experiments, listing and counting the outcomes in the sample space is easy, as in the previous examples. In other experiments, especially those consisting of several stages, you will have to rely on counting techniques to determine the number of outcomes in the sample space.
EXAMPLE: Standard decks of 52 playing cards consists of four suits: clubs ♣, spades ♠, hearts ♥, and diamonds ♦. Clubs and spades are black-colored suits; hearts and diamonds are red-colored suits. Each suit has 13 cards consisting of 3 face cards (king, queen, and jack) and number cards from 1 (ace) to 10.

Consider the experiment of drawing 5 cards at random from a well-shuffled deck of 52 playing cards. How many outcomes are in the sample space of this experiment?
SOLUTION: Since the order in which the five cards are arranged after they are drawn is not important in the problem, this is a combination problem. You want to know how many different 5-card combinations are possible when drawing from a deck of 52 playing cards. Therefore, you need to calculate the combination of 5 items selected from 52 distinct items
Thus, in the experiment of drawing 5 cards from a standard deck of 52 playing cards, the number of outcomes in the sample space is 2,598,960.